You know those mind-blowing maths tricks shared all over social media? As teachers, you either love them or cringe when you see them!
As we know, some of these tricks or ‘shortcuts’ will only work under particular circumstances, which is not often explained to students, causing a lot of confusion when the ‘trick’ doesn’t work.
A lot of research suggests that it’s ok to teach these maths tricks to your students once they have mastered that particular mathematical concept.
Why not introduce the trick and discuss it, experiment with it, let them pull it apart and try and work out how it works?
Here are four ‘tricks’ or ‘shortcuts’ I think are worth exploring in the classroom. Some of them are not ‘quick’ but definitely fun! Is there anything wrong with getting kids excited about maths?
Easy Subtraction with No Grouping
Once your students have an understanding of how to do subtraction with regrouping (borrowing), this little shortcut is a great ‘trick’ to teach your students!
You can introduce the concept of looking at subtraction as the distance between two numbers.
So, if you look at the numbers 4000 and 1394, the distance between those two numbers is the same as the distance between 3999 and 1393. Therefore, if you are provided with the sum 4000-1394, you can subtract 1 from each of those numbers and subtract 1393 from 3999 to get the same answer.
Obviously, you are not going to always subtract 1, it’s only if you need to make the top number (or most of the digits in that number) smaller to decrease the amount of ‘borrowing’ and ‘grouping’ you have to do.
A great conversation to have with your students to discuss why or why not it is worth subtracting the 1 first.


Note: Some subtraction problems may not be an easy subtract 1 scenario. For example 652 – 198. Taking 1 off each of these numbers doesn’t result in an easier subtraction sum. Instead, you could simply subtract 3 to make it easier. There is still some regrouping needed however, it’s not as difficult.
How to Compare Fractions Easily
Fractions can get really confusing, especially when students need to compare two of them and they don’t have the same denominator.
There is a really cool trick to help figure out which fraction is the larger. By multiplying the top number of each fraction by the bottom number of the other fraction you can easily get the answer.
This is also called ‘cross multiplying’ because you create a cross in the middle.

The numbers that you get from cross multiplying fractions become the two numerators you would get if your students had gone through the process of creating two ‘like’ fractions. All they need to do now is work out the bigger number of the two!

Japanese Multiplication
Have you seen this multiplication method? It’s basically taking a multiplication problem and turning it into a simple counting problem that we can solve visually.
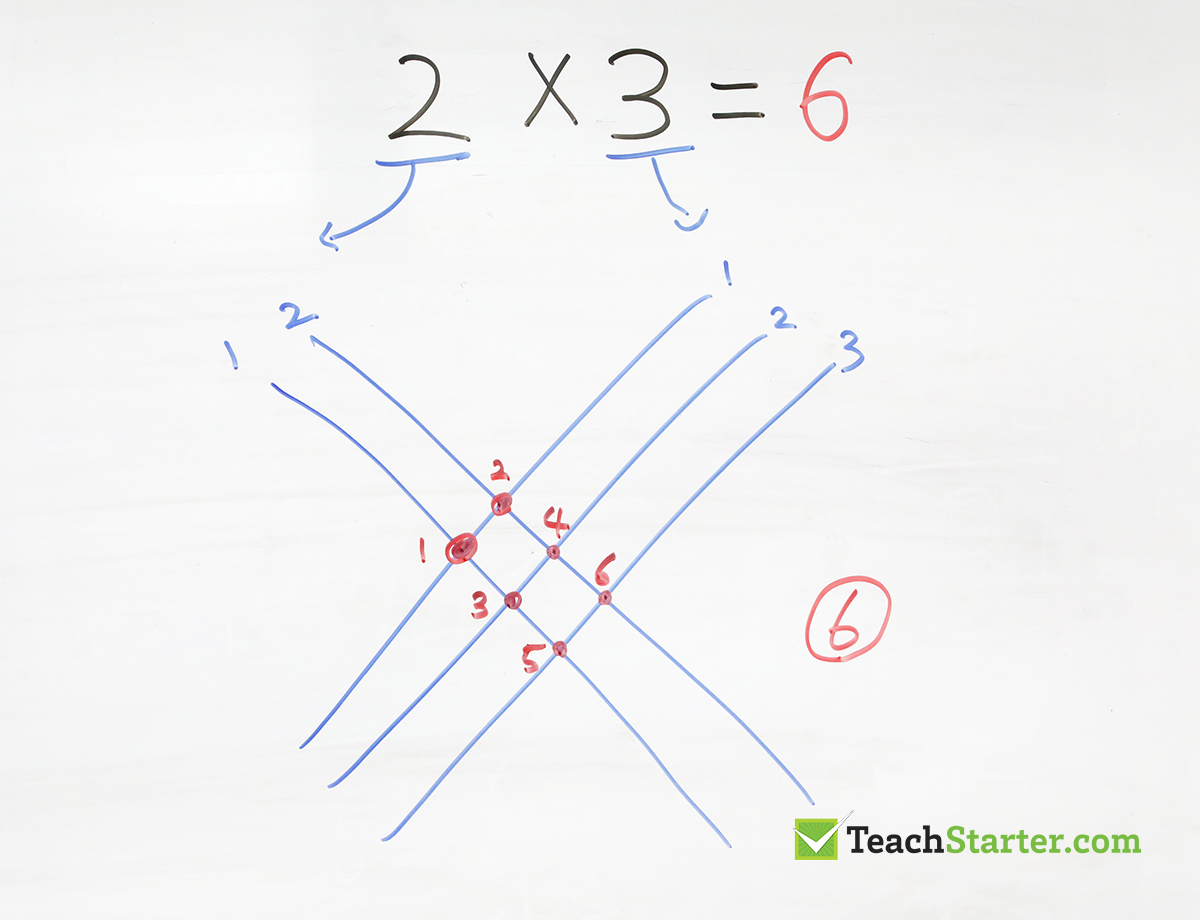
Let’s look at a really simple multiplication sum to start with. Basically, you are looking at 2 x 3, or 2 groups of 3.
By drawing 2 lines one way and 3 lines the other. You are creating an intersection of 2 groups of 3, giving you the answer of 6.
Perhaps a little tedious when you are looking at a simple multiplication like this. But, it’s a great way to start looking at this method before you move to larger numbers.

By counting all of the times the lines intersect you get your answer to this simple multiplication sum.
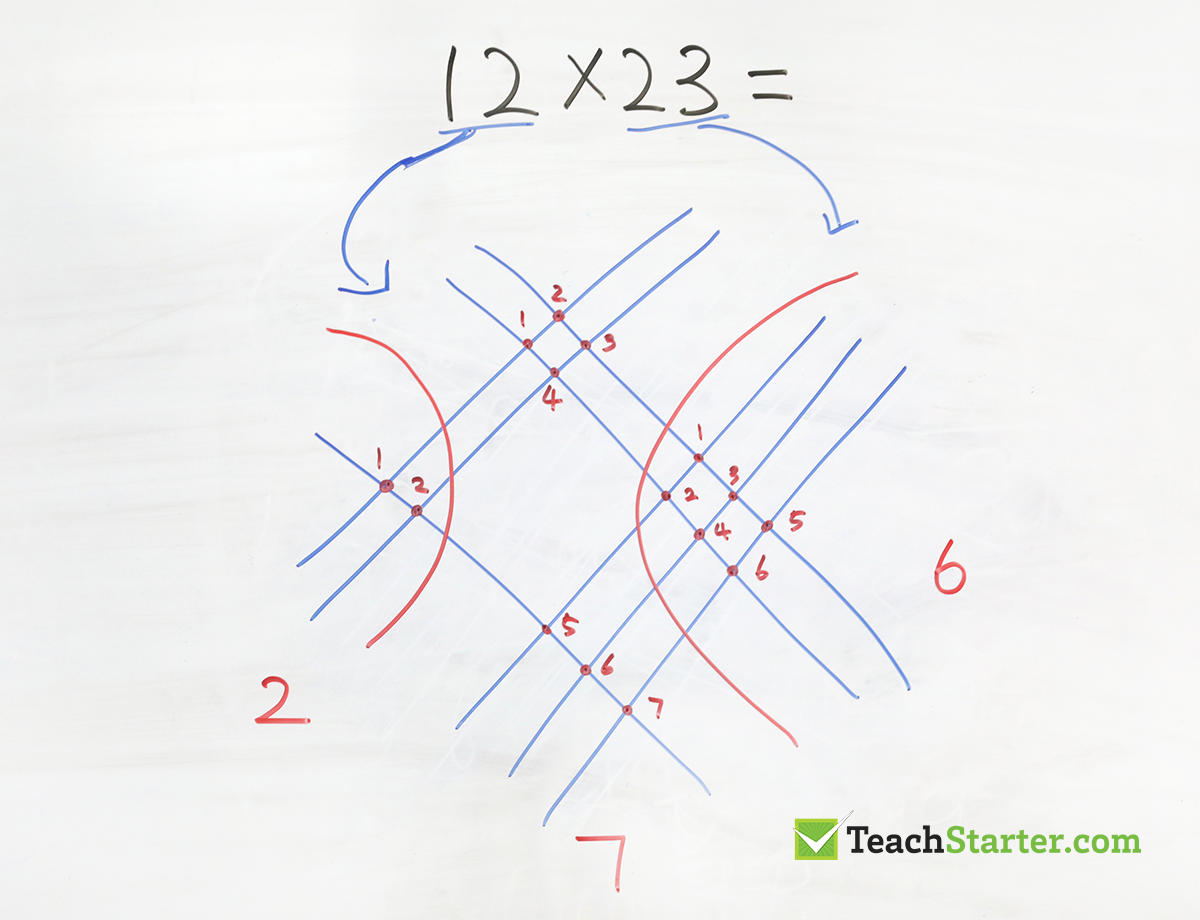
Now, let’s try a trickier multiplication sum.
- Each place value number in both numbers requires a set of lines.
- The 1 line for the number 1 in 12 is representing (1) ten.
- The 2 lines (going the same way), simply represents (2) ones.
- With the number 23. The 2 lines (going the other way) represent the (2) tens and the 3 lines represent the (3) ones.
- You need to make sure that both numbers you are multiplying, crossover like the image below.

On the left corner, put a curved line through the wide spot with no points and do the same on the right. Separating the intersections into three groups.
Then, you count the three groups of intersections, giving you the answer of 276.
How does Japanese Multiplication work?
I’m going to try my best to explain the maths behind this method for multiplying numbers, here goes…
- Remember, we are looking at the sum 12 x 23
- Let’s start with the intersections on the far right. There are 6 intersections, which represents 2 ones x 3 ones. So 6 will be in our ones place for the answer.
- On the far left, there are 2 intersections, now remember, this set of lines represents the tens in the original numbers used in the sum. So 2 is 20 and 1 is 10. Meaning 20 x 10 equals 200. So, our answer will begin with the number 2 in the hundreds place.
- In the top middle section, we have 2 tens x 2 ones which gives us 40. Plus, in the bottom middle section, we have 1 ten x 3 ones which gives us 30. Giving us a total of 70 for the tens place.
- All of this gives us a grand total of 276!
- Comprehendō?
Multiplying Double Digit Numbers by 11
To multiply any two-digit numbers by 11, simply add the digits of the number together and then put this sum between the original two digits.
For example, to quickly find the answer to 26 x 11, start by adding the two digits of the number 26 together to get 2+6=8.
Next, put this new number between the original two digits to get 286. That’s the answer!
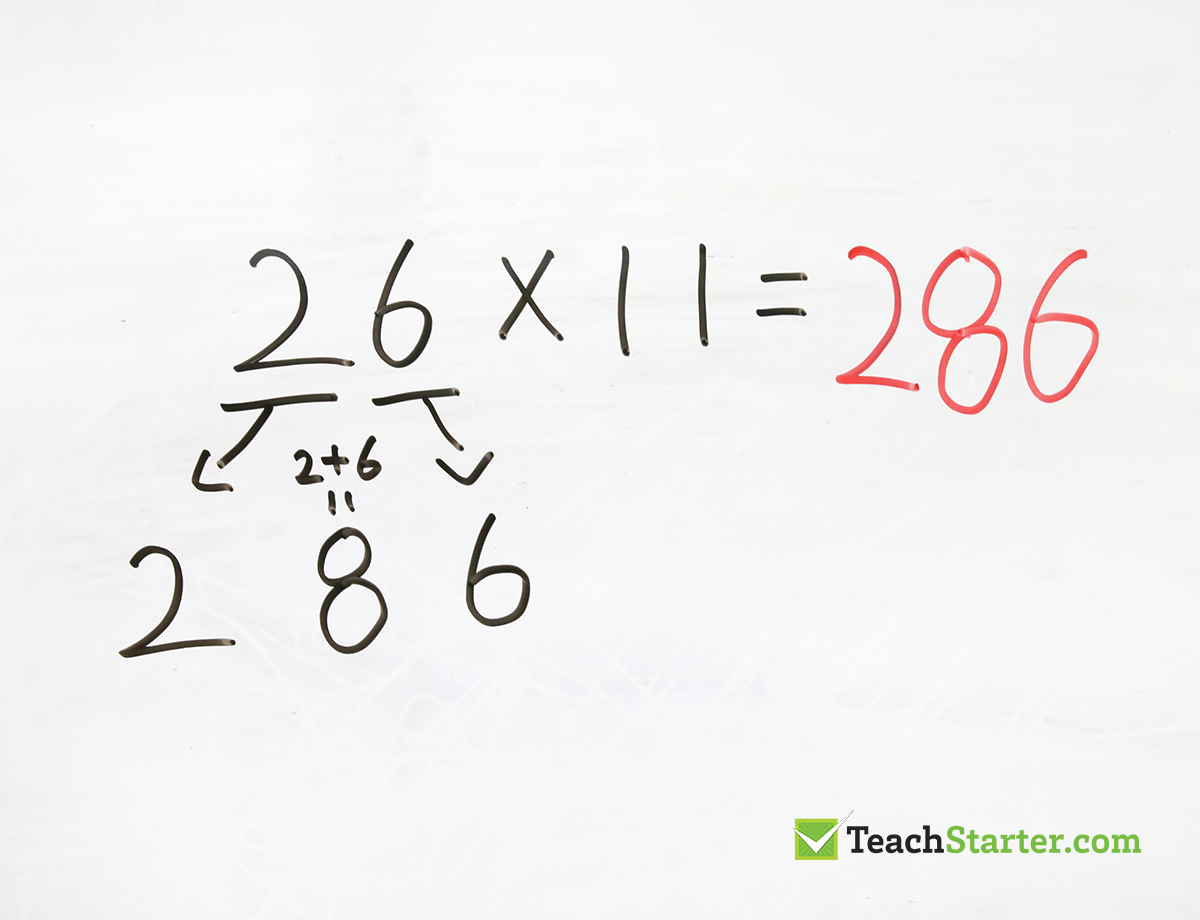
If the sum of the two digits is greater than 9, simply carry the 1 over to the tens digit.
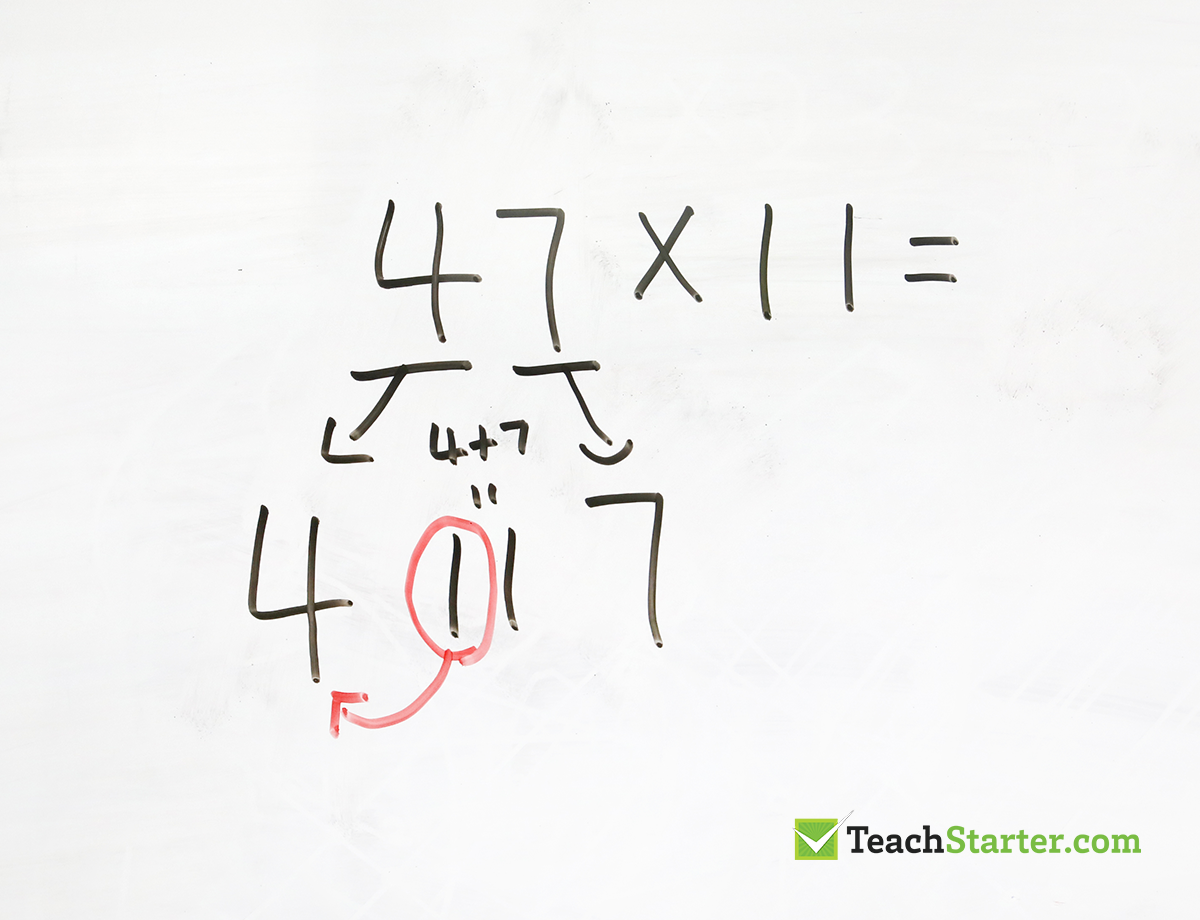
In this example, the 1 is carried over to the 4 resulting in the answer of 517.
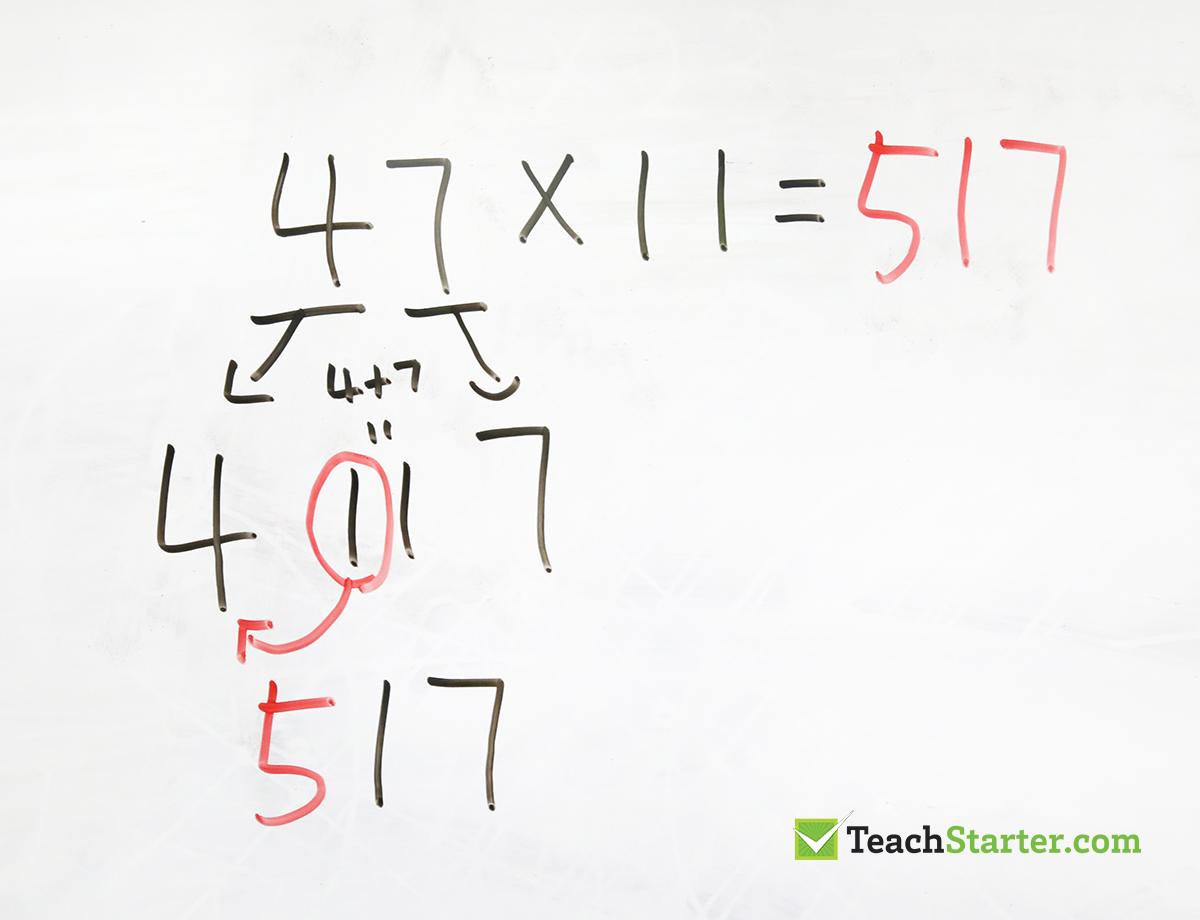






Comments