21 Numeracy Exit Ticket activities for students to provide evidence of their learning progress.
This teaching resource is an assessment tool for students to show evidence of their learning. Use Exit Tickets after a numeracy skill has been taught to show evidence that students have acquired the skill and are ready to move forward to the next learning goal.
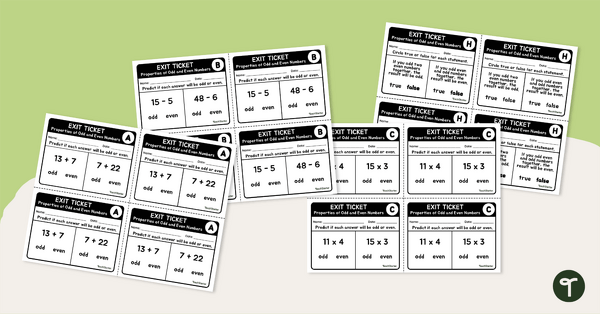
These Numeracy Exit tickets collect evidence for basic Year 3 curriculum requirements. Use the editable Word version to create your own class-specific learning goals.











There is an error in the web copy for this resource. It uses they as a pronoun without specifying a subject and needs an 'are' before ready. 'Use Exit Tickets after a numeracy skill has been taught, as a way to show evidence that STUDENTS have acquired the skill and ARE ready to move forward to the next learning goal.
Hi Roberta, Thank you for letting us know! The resource description has been updated. If we can assist with anything else, please don't hesitate to contact us.