teaching resource

Build Your Own Theme Park – Project

Updated: 20 Nov 2023

A project that gives students the opportunity to learn through building their own theme park.

Editable: Word
Non-Editable: PDF
Pages: 17 Pages
Years: 4 - 6

Curriculum

ACMNA080

Solve problems involving purchases and the calculation of change to the nearest five cents with and without digital technologies
ACMMG084

Use scaled instruments to measure and compare lengths, masses, capacities and temperatures
ACMMG290

Compare objects using familiar metric units of area and volume
ACMMG090

Use simple scales, legends and directions to interpret information contained in basic maps
ACMNA106

Create simple financial plans
ACMMG108

Choose appropriate units of measurement for length, area, volume, capacity and mass
ACMMG109

Calculate perimeter and area of rectangles using familiar metric units
ACMNA132

Investigate and calculate percentage discounts of 10%, 25% and 50% on sale items, with and without digital technologies
ACMMG135

Connect decimal representations to the metric system
ACMMG136

Convert between common metric units of length, mass and capacity
ACMMG137

Solve problems involving the comparison of lengths and areas using appropriate units
ACMMG138

Connect volume and capacity and their units of measurement
ACMMG139

Interpret and use timetables
ACHASSK121

Influences on consumer choices and methods that can be used to help make informed personal consumer and financial choices
ACHASSK120

Types of resources (natural, human, capital) and the ways societies use them to satisfy the needs and wants of present and future generationsElaborationscategorising resources as natural (water, coal, wheat), human (workers, business owners, designin...
ACHASSK151

The reasons businesses exist and the different ways they provide goods and servicesElaborationsidentifying why businesses exist (for example, to produce goods and services, to make a profit, to provide employment) and investigating the different ways...
ACHASSK150

The effect that consumer and financial decisions can have on the individual, the broader community and the environment
ACTDEP015

Generate, develop, and communicate design ideas and decisions using appropriate technical terms and graphical representation techniques
ACTDEP017

Evaluate design ideas, processes and solutions based on criteria for success developed with guidance and including care for the environment
ACTDEP025

Generate, develop and communicate design ideas and processes for audiences using appropriate technical terms and graphical representation techniques
ACTDEP027

Negotiate criteria for success that include sustainability to evaluate design ideas, processes and solutions
ACAVAM116

Plan the display of artworks to enhance their meaning for an audience

teaching resource

Build Your Own Theme Park – Project

Updated: 20 Nov 2023

A project that gives students the opportunity to learn through building their own theme park.

Editable: Word
Non-Editable: PDF
Pages: 17 Pages
Years: 4 - 6

A project that gives students the opportunity to learn through building their own theme park.

Have you ever wanted to design your very own theme park?

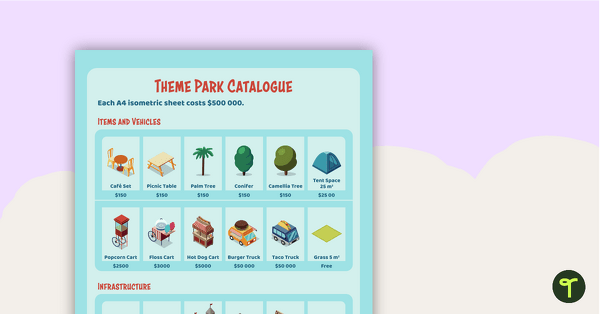
This teaching resource gives students the opportunity to learn through designing their own theme parks. In this project, students navigate a set budget and isometric awareness to plan to execute the best theme park they can design. Students will not only relate to the excitement of building a theme park, but they will also think creatively to design a theme park people would want to visit. Students can use and purchase supplied theme park rides, attractions and infrastructure, or are encouraged to design and draw their own theme park facilities on isometric paper.

In this project, students will learn about:

measurement, including length, perimeter, area, volume and scale
geometric isometrics
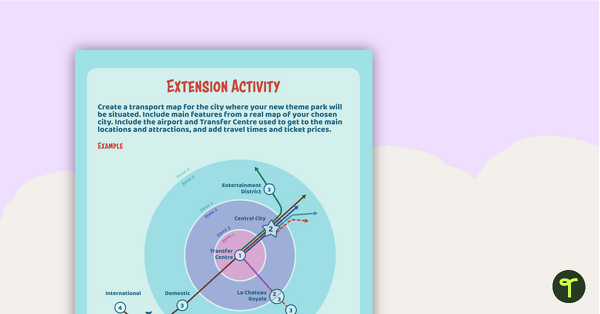
3D mapping
transport maps and time
money and budgets
technology and design
business concepts including needs of clientele

You can extend this project by:

creating a competitive class environment between individuals and groups
using currency and park features as additional rewards
restricting the budget and charging for free items.

The learning experiences are limitless!

Check out our other stimulus-related resources.

Curriculum

ACMNA080

Solve problems involving purchases and the calculation of change to the nearest five cents with and without digital technologies
ACMMG084

Use scaled instruments to measure and compare lengths, masses, capacities and temperatures
ACMMG290

Compare objects using familiar metric units of area and volume
ACMMG090

Use simple scales, legends and directions to interpret information contained in basic maps
ACMNA106

Create simple financial plans
ACMMG108

Choose appropriate units of measurement for length, area, volume, capacity and mass
ACMMG109

Calculate perimeter and area of rectangles using familiar metric units
ACMNA132

Investigate and calculate percentage discounts of 10%, 25% and 50% on sale items, with and without digital technologies
ACMMG135

Connect decimal representations to the metric system
ACMMG136

Convert between common metric units of length, mass and capacity
ACMMG137

Solve problems involving the comparison of lengths and areas using appropriate units
ACMMG138

Connect volume and capacity and their units of measurement
ACMMG139

Interpret and use timetables
ACHASSK121

Influences on consumer choices and methods that can be used to help make informed personal consumer and financial choices
ACHASSK120

Types of resources (natural, human, capital) and the ways societies use them to satisfy the needs and wants of present and future generationsElaborationscategorising resources as natural (water, coal, wheat), human (workers, business owners, designin...
ACHASSK151

The reasons businesses exist and the different ways they provide goods and servicesElaborationsidentifying why businesses exist (for example, to produce goods and services, to make a profit, to provide employment) and investigating the different ways...
ACHASSK150

The effect that consumer and financial decisions can have on the individual, the broader community and the environment
ACTDEP015

Generate, develop, and communicate design ideas and decisions using appropriate technical terms and graphical representation techniques
ACTDEP017

Evaluate design ideas, processes and solutions based on criteria for success developed with guidance and including care for the environment
ACTDEP025

Generate, develop and communicate design ideas and processes for audiences using appropriate technical terms and graphical representation techniques
ACTDEP027

Negotiate criteria for success that include sustainability to evaluate design ideas, processes and solutions
ACAVAM116

Plan the display of artworks to enhance their meaning for an audience

Teach Starter Publishing

We create premium quality, downloadable teaching resources for primary/elementary school teachers that make classrooms buzz!

4 Comments

Write a review to help other teachers and parents like yourself. If you'd like to request a change to this resource, or report an error, select the corresponding tab above.

Zola Amendolia · 4 years ago

is good I would love if u did not have to subscribe and could make a one time payment
- Trish (Teach Starter) · 4 years ago
  
  Hi Zola, thanks for sharing your feedback! I am afraid that individual purchasing is not available, but I will pass your feedback on to the team for consideration.
Caitlin Noonan · 4 years ago

LOVE this resource! Would love it in a black and white/low colour option too please.
- Paul (Teach Starter) · 4 years ago
  
  Hi Caitlin, Thanks for your feedback! Remember, you can always submit a change request to this resource using the Changes & Updates tab above. This tab can be found near the comments section. Requests are voted on by the Teach Starter community and we create the top requests.