teaching resource

Year 5 Numeracy Exit Tickets

Updated: 04 Oct 2023

20 Numeracy Exit Ticket activities for students to provide evidence of their learning progress.

Editable: Word
Non-Editable: PDF
Pages: 6 Pages
Year: 5

Curriculum

ACMNA098

Identify and describe factors and multiples of whole numbers and use them to solve problems
ACMNA099

Use estimation and rounding to check the reasonableness of answers to calculations
ACMNA100

Solve problems involving multiplication of large numbers by one- or two-digit numbers using efficient mental, written strategies and appropriate digital technologies
ACMNA101

Solve problems involving division by a one digit number, including those that result in a remainder
ACMNA291

Use efficient mental and written strategies and apply appropriate digital technologies to solve problems
ACMNA102

Compare and order common unit fractions and locate and represent them on a number line
ACMNA103

Investigate strategies to solve problems involving addition and subtraction of fractions with the same denominator
ACMNA104

Recognise that the place value system can be extended beyond hundredths
ACMNA105

Compare, order and represent decimals
ACMNA106

Create simple financial plans
ACMNA107

Describe, continue and create patterns with fractions, decimals and whole numbers resulting from addition and subtraction
ACMNA121

Find unknown quantities in number sentences involving multiplication and division and identify equivalent number sentences involving multiplication and division
ACMMG108

Choose appropriate units of measurement for length, area, volume, capacity and mass
ACMMG109

Calculate perimeter and area of rectangles using familiar metric units
ACMMG110

Compare 12- and 24-hour time systems and convert between them
ACMMG114

Describe translations, reflections and rotations of two-dimensional shapes. Identify line and rotational symmetries
ACMMG115

Apply the enlargement transformation to familiar two dimensional shapes and explore the properties of the resulting image compared with the original
ACMMG112

Estimate, measure and compare angles using degrees. Construct angles using a protractor
ACMSP116

List outcomes of chance experiments involving equally likely outcomes and represent probabilities of those outcomes using fractions
ACMSP117

Recognise that probabilities range from 0 to 1

AC9M5N01

Interpret, compare and order numbers with more than 2 decimal places, including numbers greater than one, using place value understanding; represent these on a number line
AC9M5N02

Express natural numbers as products of their factors, recognise multiples and determine if one number is divisible by another
AC9M5N03

Compare and order fractions with the same and related denominators including mixed numerals, applying knowledge of factors and multiples; represent these fractions on a number line
AC9M5N05

Solve problems involving addition and subtraction of fractions with the same or related denominators, using different strategies
AC9M5N06

Solve problems involving multiplication of larger numbers by one- or two-digit numbers, choosing efficient calculation strategies and using digital tools where appropriate; check the reasonableness of answers
AC9M5N07

Solve problems involving division, choosing efficient strategies and using digital tools where appropriate; interpret any remainder according to the context and express results as a whole number, decimal or fraction
AC9M5N08

Check and explain the reasonableness of solutions to problems including financial contexts using estimation strategies appropriate to the context
AC9M5N09

Use mathematical modelling to solve practical problems involving additive and multiplicative situations including financial contexts; formulate the problems, choosing operations and efficient calculation strategies, using digital tools where appropriate; interpret and communicate solutions in terms
AC9M5A02

Find unknown values in numerical equations involving multiplication and division using the properties of numbers and operations
AC9M5M01

Choose appropriate metric units when measuring the length, mass and capacity of objects; use smaller units or a combination of units to obtain a more accurate measure
AC9M5M02

Solve practical problems involving the perimeter and area of regular and irregular shapes using appropriate metric units
AC9M5M03

Compare 12- and 24-hour time systems and solve practical problems involving the conversion between them
AC9M5M04

Estimate, construct and measure angles in degrees, using appropriate tools including a protractor, and relate these measures to angle names
AC9M5SP03

Describe and perform translations, reflections and rotations of shapes, using dynamic geometric software where appropriate; recognise what changes and what remains the same, and identify any symmetries
AC9M5P01

List the possible outcomes of chance experiments involving equally likely outcomes and compare to those which are not equally likely
AC9M6P01

Recognise that probabilities lie on numerical scales of 0 – 1 or 0% – 100% and use estimation to assign probabilities that events occur in a given context, using common fractions, percentages and decimals

teaching resource

Year 5 Numeracy Exit Tickets

Updated: 04 Oct 2023

20 Numeracy Exit Ticket activities for students to provide evidence of their learning progress.

Editable: Word
Non-Editable: PDF
Pages: 6 Pages
Year: 5

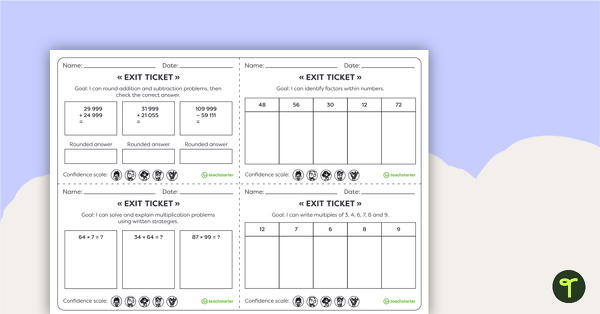
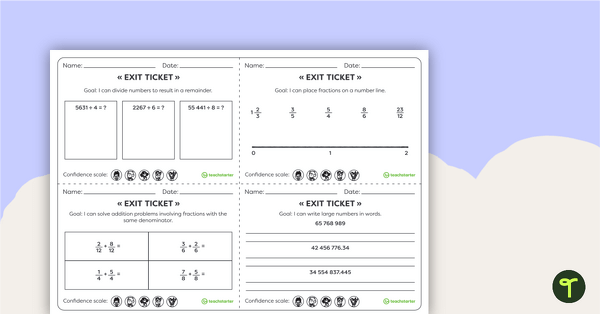
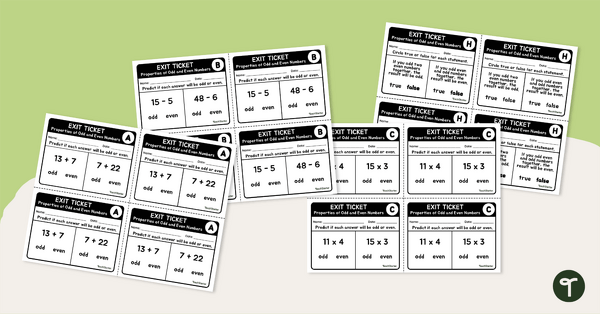
20 Numeracy Exit Ticket activities for students to provide evidence of their learning progress.

This teaching resource is an assessment tool for students to show evidence of their learning. Use Exit Tickets after a numeracy skill has been taught to show evidence that they have acquired the skill and are ready to move to the next learning goal.

These Numeracy Exit tickets collect evidence for basic Year 5 curriculum requirements. Use the editable Word version to create your own class-specific learning goals.

Curriculum

ACMNA098

Identify and describe factors and multiples of whole numbers and use them to solve problems
ACMNA099

Use estimation and rounding to check the reasonableness of answers to calculations
ACMNA100

Solve problems involving multiplication of large numbers by one- or two-digit numbers using efficient mental, written strategies and appropriate digital technologies
ACMNA101

Solve problems involving division by a one digit number, including those that result in a remainder
ACMNA291

Use efficient mental and written strategies and apply appropriate digital technologies to solve problems
ACMNA102

Compare and order common unit fractions and locate and represent them on a number line
ACMNA103

Investigate strategies to solve problems involving addition and subtraction of fractions with the same denominator
ACMNA104

Recognise that the place value system can be extended beyond hundredths
ACMNA105

Compare, order and represent decimals
ACMNA106

Create simple financial plans
ACMNA107

Describe, continue and create patterns with fractions, decimals and whole numbers resulting from addition and subtraction
ACMNA121

Find unknown quantities in number sentences involving multiplication and division and identify equivalent number sentences involving multiplication and division
ACMMG108

Choose appropriate units of measurement for length, area, volume, capacity and mass
ACMMG109

Calculate perimeter and area of rectangles using familiar metric units
ACMMG110

Compare 12- and 24-hour time systems and convert between them
ACMMG114

Describe translations, reflections and rotations of two-dimensional shapes. Identify line and rotational symmetries
ACMMG115

Apply the enlargement transformation to familiar two dimensional shapes and explore the properties of the resulting image compared with the original
ACMMG112

Estimate, measure and compare angles using degrees. Construct angles using a protractor
ACMSP116

List outcomes of chance experiments involving equally likely outcomes and represent probabilities of those outcomes using fractions
ACMSP117

Recognise that probabilities range from 0 to 1

AC9M5N01

Interpret, compare and order numbers with more than 2 decimal places, including numbers greater than one, using place value understanding; represent these on a number line
AC9M5N02

Express natural numbers as products of their factors, recognise multiples and determine if one number is divisible by another
AC9M5N03

Compare and order fractions with the same and related denominators including mixed numerals, applying knowledge of factors and multiples; represent these fractions on a number line
AC9M5N05

Solve problems involving addition and subtraction of fractions with the same or related denominators, using different strategies
AC9M5N06

Solve problems involving multiplication of larger numbers by one- or two-digit numbers, choosing efficient calculation strategies and using digital tools where appropriate; check the reasonableness of answers
AC9M5N07

Solve problems involving division, choosing efficient strategies and using digital tools where appropriate; interpret any remainder according to the context and express results as a whole number, decimal or fraction
AC9M5N08

Check and explain the reasonableness of solutions to problems including financial contexts using estimation strategies appropriate to the context
AC9M5N09

Use mathematical modelling to solve practical problems involving additive and multiplicative situations including financial contexts; formulate the problems, choosing operations and efficient calculation strategies, using digital tools where appropriate; interpret and communicate solutions in terms
AC9M5A02

Find unknown values in numerical equations involving multiplication and division using the properties of numbers and operations
AC9M5M01

Choose appropriate metric units when measuring the length, mass and capacity of objects; use smaller units or a combination of units to obtain a more accurate measure
AC9M5M02

Solve practical problems involving the perimeter and area of regular and irregular shapes using appropriate metric units
AC9M5M03

Compare 12- and 24-hour time systems and solve practical problems involving the conversion between them
AC9M5M04

Estimate, construct and measure angles in degrees, using appropriate tools including a protractor, and relate these measures to angle names
AC9M5SP03

Describe and perform translations, reflections and rotations of shapes, using dynamic geometric software where appropriate; recognise what changes and what remains the same, and identify any symmetries
AC9M5P01

List the possible outcomes of chance experiments involving equally likely outcomes and compare to those which are not equally likely
AC9M6P01

Recognise that probabilities lie on numerical scales of 0 – 1 or 0% – 100% and use estimation to assign probabilities that events occur in a given context, using common fractions, percentages and decimals

Teach Starter Publishing

We create premium quality, downloadable teaching resources for primary/elementary school teachers that make classrooms buzz!

4 Comments

Write a review to help other teachers and parents like yourself. If you'd like to request a change to this resource, or report an error, select the corresponding tab above.

Zuriette Du Plessis · 4 years ago

Thank you for another helpful resource. These Exit Tickets can be useful for pre- and post testing or fast finisher work.
- Paul (Teach Starter) · 4 years ago
  
  You're most welcome, Zuriette! Thank you for sharing your tip on how the exit tickets can be used!
ST Mary MacKillop College · 4 years ago

I love the idea of Exit tickets and am going to use them this semester. Are you planning to create more please?
- Janeen · 4 years ago
  
  Hi ST Mary MacKillop College Thanks for getting in touch with us! Might I suggest that you make a new resource request and list specifically what you were after? You can do so on our Requests page. https://www.teachstarter.com/request-a-resource/ Your fellow Teach Starter members can then vote for it and, if it proves popular, we would love to make it for you! Kind regards Janeen