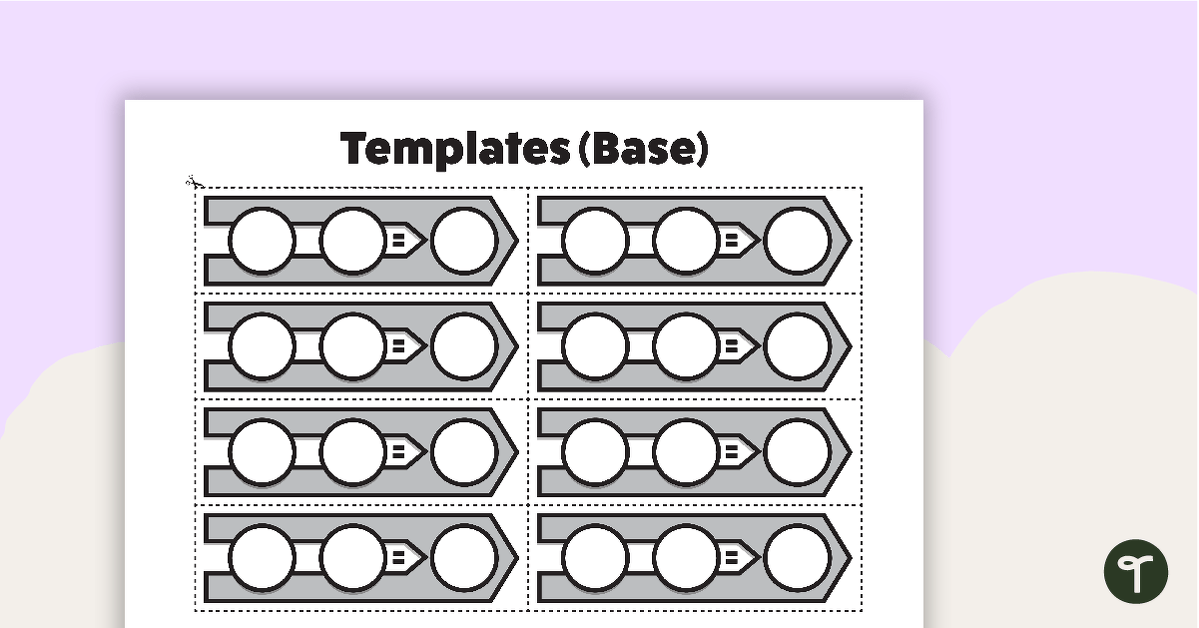
A versatile set of templates that can be used for number sentences and much more.
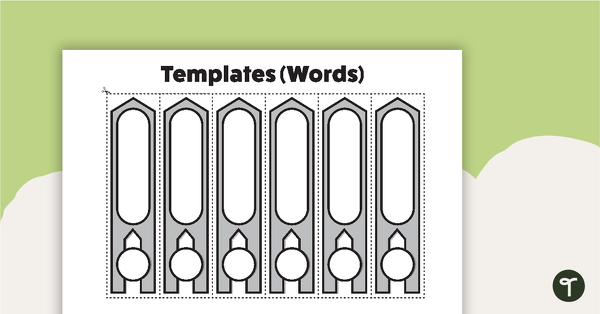
Use these number sentence strips when exploring mathematical operations or when building words using individual sounds.
They can be used as a scaffold for students when representing a word problem as a number sentence or labelling an array of objects.
Students can stick the strips in their workbooks to act as labels pointing to another representation of the answer.
The resource includes:
- base templates
- base template extensions (use these to add additional numbers to number sentences)
- extension templates with a larger answer box (use these for larger numbers or words)
- circle templates (use these for cutting and pasting numbers or letters onto the template).











0 Comments
Write a review to help other teachers and parents like yourself. If you'd like to request a change to this resource, or report an error, select the corresponding tab above.