A numeral expander template to use when exploring five-digit numbers.
Use this numeral expander to explore the place value of numbers in the tens of thousands.
teaching resource
Numeral Expander - Tens of Thousands
Updated: 28 Sep 2023
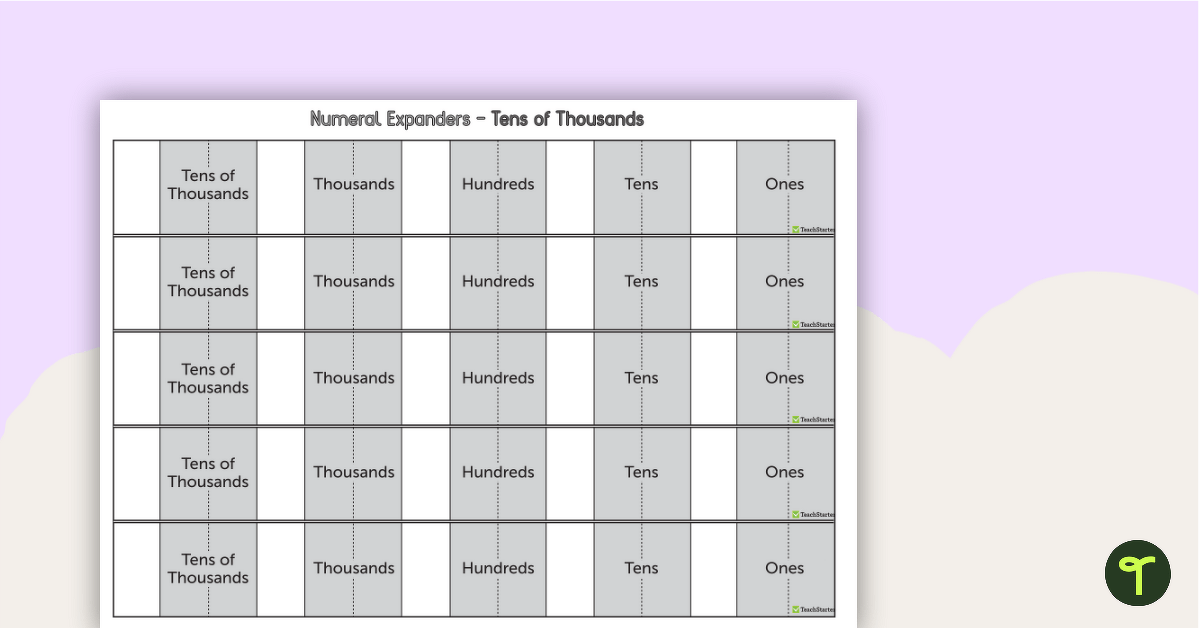
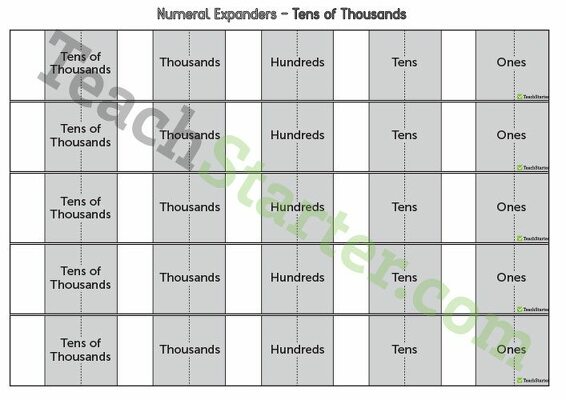
A numeral expander template to use when exploring five-digit numbers.
Non-Editable: PDF
Pages: 1 Page
Years: 3 - 4
Curriculum
ACMNA052
Recognise, model, represent and order numbers to at least 10 000
ACMNA053
Apply place value to partition, rearrange and regroup numbers to at least 10 000 to assist calculations and solve problems
ACMNA072
Recognise, represent and order numbers to at least tens of thousands
ACMNA073
Apply place value to partition, rearrange and regroup numbers to at least tens of thousands to assist calculations and solve problems
MA2-4NA
WholeNumbers - applies place value to order, read and represent numbers of up to five digits
VCMNA130
Recognise, model, represent and order numbers to at least 10 000
VCMNA131
Apply place value to partition, rearrange and regroup numbers to at least 10 000 to assist calculations and solve problems
VCMNA152
Recognise, represent and order numbers to at least tens of thousands
VCMNA153
Apply place value to partition, rearrange and regroup numbers to at least tens of thousands to assist calculations and solve problems
AC9M3N01
Recognise, represent and order natural numbers using naming and writing conventions for numerals beyond 10 000
AC9M3N03
Add and subtract two- and three-digit numbers using place value to partition, rearrange and regroup numbers to assist in calculations without a calculator
AC9M4N06
Develop efficient strategies and use appropriate digital tools for solving problems involving addition and subtraction, and multiplication and division where there is no remainder
Curriculum
ACMNA052
Recognise, model, represent and order numbers to at least 10 000
ACMNA053
Apply place value to partition, rearrange and regroup numbers to at least 10 000 to assist calculations and solve problems
ACMNA072
Recognise, represent and order numbers to at least tens of thousands
ACMNA073
Apply place value to partition, rearrange and regroup numbers to at least tens of thousands to assist calculations and solve problems
MA2-4NA
WholeNumbers - applies place value to order, read and represent numbers of up to five digits
VCMNA130
Recognise, model, represent and order numbers to at least 10 000
VCMNA131
Apply place value to partition, rearrange and regroup numbers to at least 10 000 to assist calculations and solve problems
VCMNA152
Recognise, represent and order numbers to at least tens of thousands
VCMNA153
Apply place value to partition, rearrange and regroup numbers to at least tens of thousands to assist calculations and solve problems
AC9M3N01
Recognise, represent and order natural numbers using naming and writing conventions for numerals beyond 10 000
AC9M3N03
Add and subtract two- and three-digit numbers using place value to partition, rearrange and regroup numbers to assist in calculations without a calculator
AC9M4N06
Develop efficient strategies and use appropriate digital tools for solving problems involving addition and subtraction, and multiplication and division where there is no remainder
Teach Starter Publishing
We create premium quality, downloadable teaching resources for primary/elementary school teachers that make classrooms buzz!
4 Comments
Write a review to help other teachers and parents like yourself. If you'd like to request a change to this resource, or report an error, select the corresponding tab above.
Log in
to comment
Suggest a Change
Would you like something changed or customised on this resource? While our team makes every effort to complete change suggestions, we can't guarantee that every change will be completed.
Login
to suggest a change
Report an Error
Did you spot an error on this resource? Please let us know and we will fix it shortly.
Login
to report an error
Help
Are you having trouble downloading or viewing this resource? Please try the following steps:
- Check that you are logged in to your account
- For premium resources, check that you have a paid subscription
- Check that you have installed Adobe Reader ( download here )
If you are still having difficulty, please visit the Teach Starter Help Desk or contact us .
You may also like
- Plus Plan
5-Digit Place Value Warm Up - Interactive PowerPoint
An engaging 44 slide interactive PowerPoint to use when learning about place value to 5-digits.
- Plus Plan
Exploring 4-Digit Place Value PowerPoint
A 31 slide PowerPoint template to use when exploring place value to thousands.
- Plus Plan
4-Digit Place Value - Assessment
An open-ended worksheet to use when assessing your students' knowledge of place value to the thousands.
- Plus Plan
5-Digit Place Value - Assessment
An open-ended worksheet to use when assessing your students' knowledge of place value to the tens of thousands.
- Plus Plan
Roll It, Make It, Expand It! - Place Value Worksheet
A worksheet for students to use when learning about the place value of two-digit numbers.
- Plus Plan
Representing Two-Digit Numbers - Place Value Worksheet
A set of worksheets for students to use when learning about place value and the different way two-digit numbers can be represented.
- Plus Plan
Exploring 2-Digit Place Value PowerPoint
Explore 2-digit numbers using place value strategies with an interactive teaching presentation.
- Plus Plan
3-Digit Number of the Day Worksheet
A 3-digit place value worksheet to represent the number of the day in different ways.
- Plus Plan
Place Value STEM Challenge - Number Forms
Show numbers in picture, word, and expanded forms with an engaging Place Value S.T.E.M. Activity!
- Plus Plan
3-Digit Place Value Warm Up - Interactive PowerPoint
An engaging 44 slide interactive PowerPoint to use when learning about place value to 3-digits.
Would love this to be also available in just tens and ones and hundreds, tens and ones for the junior years :)
Hi Kodey, Thanks for your suggestion. Please feel free to request a resource here: https://www.teachstarter.com/request-a-resource/ Requests are voted on by the Teach Starter community. We create the top request each week. Please let me know if you have any further questions, I'm more than happy to help.
this would be useful if it also looked at decimals. eg. including tenths, hundredths, etc.
Hi Anne-Maree, Thank you for your suggestion. If you would like us to create this resource for you, you can formally request this here: https://www.teachstarter.com/request-a-resource/ Kind regards, Steph