teaching resource

Multiplication Facts PowerPoint - One Times Tables

Teach Starter Publishing
PowerPoint, PDF | 30 pages | Years: 2 - 7

A 30 slide PowerPoint to use when learning about multiplication.

Use this PowerPoint presentation when teaching multiplication facts. This teaching resource covers the one times tables up to fourteen, featuring a combination of number and word problems. An answer slide is provided for each question, demonstrating an array and number sentence.

Use this PowerPoint as a warm up at the beginning of your lesson or as an enrichment task for early finishers.

This resource forms part of the Multiplication PowerPoint Resource Collection.

 

Curriculum

Author

Photo of Nikki (Teach Starter)
Nikki (Teach Starter)
Photo of Fleur (Teach Starter)
Designed by Fleur (Teach Starter)
Teach Starter Publishing

Teach Starter Publishing

We create premium quality, downloadable teaching resources for primary/elementary school teachers that make classrooms buzz!

Find more resources like this

2 Comments

Write a review to help other teachers and parents like yourself. If you'd like to request a change to this resource, or report an error, select the corresponding tab above.

Login to comment
  • Renae Guelfi
    ·

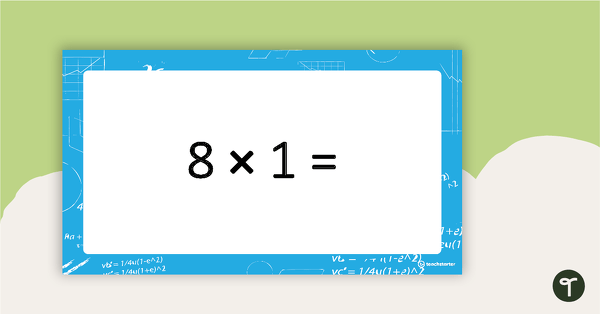
    I would love to see these powerpoints for division facts/multiples

    • Kristian
      ·

      Hi Renae, thanks for your suggestion. Please feel free to suggest it via the Request a Resource section: https://www.teachstarter.com/request-a-resource/ Your request will be voted on by the community. Each week, our team creates the most popular request. If your request hits the top of the list, we’ll be happy to make it for you!