A worksheet to use when learning the multiplication facts of eleven.
Use this teaching resource when teaching and learning the multiplication facts of eleven.
Updated: 14 Sep 2018
A worksheet to use when learning the multiplication facts of eleven.
Non-Editable: PDF
Pages: 1 Page
Years: 3 - 4
Tag #TeachStarter on Instagram for a chance to be featured!

A worksheet to use when learning the multiplication facts of eleven.
Use this teaching resource when teaching and learning the multiplication facts of eleven.

We create premium quality, downloadable teaching resources for primary/elementary school teachers that make classrooms buzz!
Would you like something changed or customised on this resource? While our team makes every effort to complete change suggestions, we can't guarantee that every change will be completed.
Did you spot an error on this resource? Please let us know and we will fix it shortly.
Are you having trouble downloading or viewing this resource? Please try the following steps:
If you are still having difficulty, please visit the Teach Starter Help Desk or contact us .
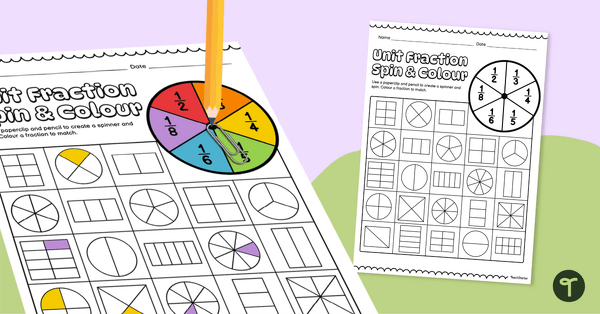
Read and colour unit fractions in this fun spin and colour activity with your students.

Engage with different unit fractions using this fun interactive flipbook for your students.

Sort and match fairy bread model cards to the corresponding unit fraction cards.

Print a set of open number lines to help you teach a variety of maths skills.

Review a variety of place value and number sense standards with a daily spiral maths review worksheet.

Estimate units of mass, volume, temperature, length, and more with an engaging, interactive measurement game.

Introduce your students to the history of the clock, time zones, and telling time with an interactive teaching presentation.

Estimate the units needed to measure capacity with an Interactive Measurement Game!

Engage your students with exciting telling time practise activities with a set of printable Time to the Hour and Half Hour Maths Mazes.

Assess your student's abilities to tell time to the nearest five minutes with a printable telling time assessment.
0 Comments
Write a review to help other teachers and parents like yourself. If you'd like to request a change to this resource, or report an error, select the corresponding tab above.