teaching resource

Year 6 Numeracy Exit Tickets – Worksheets

Updated: 03 Oct 2023

23 Numeracy Exit Ticket activities for students to provide evidence of their learning progress.

Editable: Word
Non-Editable: PDF
Pages: 1 Page
Year: 6

Curriculum

ACMNA122

Identify and describe properties of prime, composite, square and triangular numbers
ACMNA123

Select and apply efficient mental and written strategies and appropriate digital technologies to solve problems involving all four operations with whole numbers
ACMNA124

Investigate everyday situations that use integers. Locate and represent these numbers on a number line
ACMNA125

Compare fractions with related denominators and locate and represent them on a number line
ACMNA126

Solve problems involving addition and subtraction of fractions with the same or related denominators
ACMNA127

Find a simple fraction of a quantity where the result is a whole number, with and without digital technologies
ACMNA128

Add and subtract decimals, with and without digital technologies, and use estimation and rounding to check the reasonableness of answers
ACMNA129

Multiply decimals by whole numbers and perform divisions by non-zero whole numbers where the results are terminating decimals, with and without digital technologies
ACMNA130

Multiply and divide decimals by powers of 10
ACMNA131

Make connections between equivalent fractions, decimals and percentages
ACMNA133

Continue and create sequences involving whole numbers, fractions and decimals. Describe the rule used to create the sequence
ACMNA134

Explore the use of brackets and order of operations to write number sentences
ACMMG135

Connect decimal representations to the metric system
ACMMG136

Convert between common metric units of length, mass and capacity
ACMMG137

Solve problems involving the comparison of lengths and areas using appropriate units
ACMMG138

Connect volume and capacity and their units of measurement
ACMMG139

Interpret and use timetables
ACMMG142

Investigate combinations of translations, reflections and rotations, with and without the use of digital technologies
ACMMG143

Introduce the Cartesian coordinate system using all four quadrants
ACMMG141

Investigate, with and without digital technologies, angles on a straight line, angles at a point and vertically opposite angles. Use results to find unknown angles
ACMSP144

Describe probabilities using fractions, decimals and percentages

AC9M5N04

Recognise that 100% represents the complete whole and use percentages to describe, represent and compare relative size; connect familiar percentages to their decimal and fraction equivalents
AC9M6N01

Recognise situations, including financial contexts, that use integers; locate and represent integers on a number line and as coordinates on the Cartesian plane
AC9M6N02

Identify and describe the properties of prime, composite and square numbers and use these properties to solve problems and simplify calculations
AC9M6N03

Apply knowledge of equivalence to compare, order and represent common fractions including halves, thirds and quarters on the same number line and justify their order
AC9M6N04

Apply knowledge of place value to add and subtract decimals, using digital tools where appropriate; use estimation and rounding to check the reasonableness of answers
AC9M6N05

Solve problems involving addition and subtraction of fractions using knowledge of equivalent fractions
AC9M6N06

Multiply and divide decimals by multiples of powers of 10 without a calculator, applying knowledge of place value and proficiency with multiplication facts; using estimation and rounding to check the reasonableness of answers
AC9M6N07

Solve problems that require finding a familiar fraction, decimal or percentage of a quantity, including percentage discounts, choosing efficient calculation strategies and using digital tools where appropriate
AC9M6N08

Approximate numerical solutions to problems involving rational numbers and percentages, including financial contexts, using appropriate estimation strategies
AC9M6N09

Use mathematical modelling to solve practical problems, involving rational numbers and percentages, including in financial contexts; formulate the problems, choosing operations and efficient calculation strategies, and using digital tools where appropriate; interpret and communicate solutions in te
AC9M6A01

Recognise and use rules that generate visually growing patterns and number patterns involving rational numbers
AC9M6A02

Find unknown values in numerical equations involving brackets and combinations of arithmetic operations, using the properties of numbers and operations
AC9M6M01

Convert between common metric units of length, mass and capacity; choose and use decimal representations of metric measurements relevant to the context of a problem
AC9M6M02

Establish the formula for the area of a rectangle and use it to solve practical problems
AC9M6M03

Interpret and use timetables and itineraries to plan activities and determine the duration of events and journeys
AC9M6M04

Identify the relationships between angles on a straight line, angles at a point and vertically opposite angles; use these to determine unknown angles, communicating reasoning
AC9M6SP02

Locate points in the 4 quadrants of a Cartesian plane
AC9M6SP03

Recognise and use combinations of transformations to create tessellations and other geometric patterns, using dynamic geometric software where appropriate
AC9M6P01

Recognise that probabilities lie on numerical scales of 0 – 1 or 0% – 100% and use estimation to assign probabilities that events occur in a given context, using common fractions, percentages and decimals

teaching resource

Year 6 Numeracy Exit Tickets – Worksheets

Updated: 03 Oct 2023

23 Numeracy Exit Ticket activities for students to provide evidence of their learning progress.

Editable: Word
Non-Editable: PDF
Pages: 1 Page
Year: 6

23 Numeracy Exit Ticket activities for students to provide evidence of their learning progress.

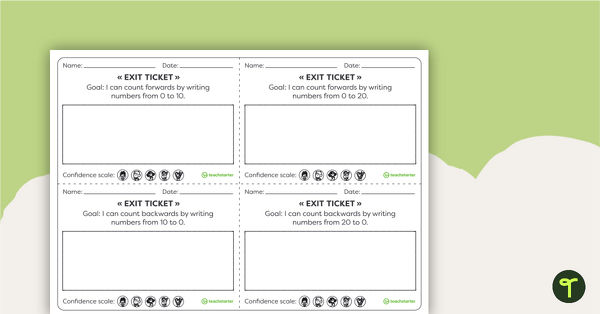
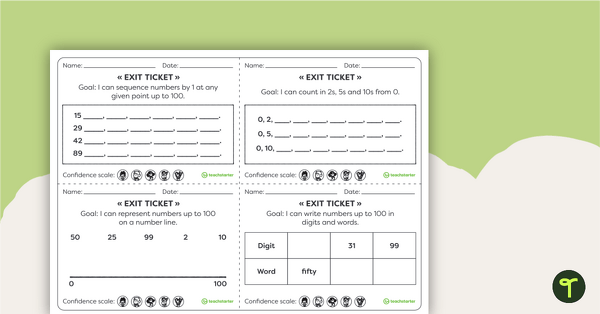
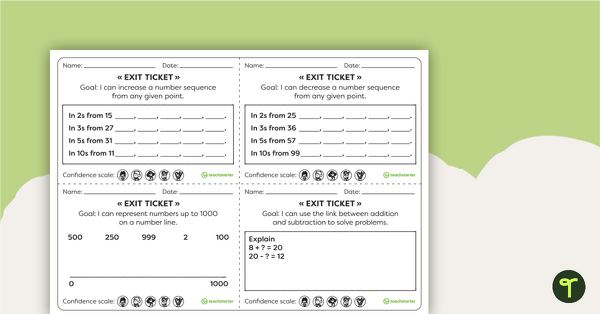
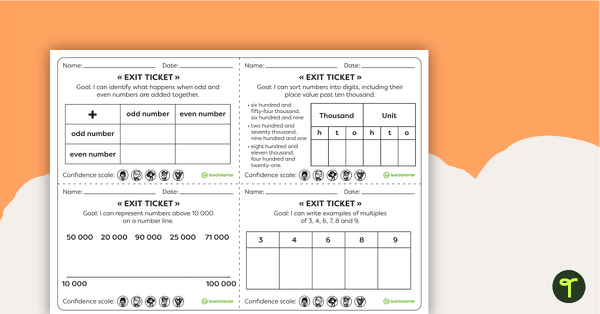
This teaching resource is an assessment tool for students to show evidence of their learning. Use Exit Tickets after a numeracy skill has been taught to show evidence that they have acquired the skill and are ready to move to the next learning goal.

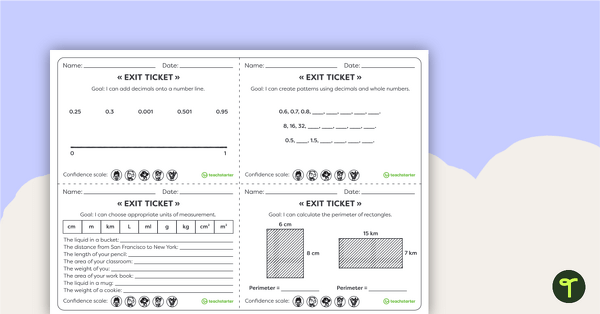
These Numeracy Exit tickets collect evidence for basic Year 6 curriculum requirements. For the prepopulated exit ticket, use the dropdown arrow on the Download button and select the PDF version of the resource. Choose the editable Word version to create your own class-specific exit ticket.

NOTE: Please note that the Word version of this exit ticket will be blank so that you can create your own class-specific exit ticket.

Curriculum

ACMNA122

Identify and describe properties of prime, composite, square and triangular numbers
ACMNA123

Select and apply efficient mental and written strategies and appropriate digital technologies to solve problems involving all four operations with whole numbers
ACMNA124

Investigate everyday situations that use integers. Locate and represent these numbers on a number line
ACMNA125

Compare fractions with related denominators and locate and represent them on a number line
ACMNA126

Solve problems involving addition and subtraction of fractions with the same or related denominators
ACMNA127

Find a simple fraction of a quantity where the result is a whole number, with and without digital technologies
ACMNA128

Add and subtract decimals, with and without digital technologies, and use estimation and rounding to check the reasonableness of answers
ACMNA129

Multiply decimals by whole numbers and perform divisions by non-zero whole numbers where the results are terminating decimals, with and without digital technologies
ACMNA130

Multiply and divide decimals by powers of 10
ACMNA131

Make connections between equivalent fractions, decimals and percentages
ACMNA133

Continue and create sequences involving whole numbers, fractions and decimals. Describe the rule used to create the sequence
ACMNA134

Explore the use of brackets and order of operations to write number sentences
ACMMG135

Connect decimal representations to the metric system
ACMMG136

Convert between common metric units of length, mass and capacity
ACMMG137

Solve problems involving the comparison of lengths and areas using appropriate units
ACMMG138

Connect volume and capacity and their units of measurement
ACMMG139

Interpret and use timetables
ACMMG142

Investigate combinations of translations, reflections and rotations, with and without the use of digital technologies
ACMMG143

Introduce the Cartesian coordinate system using all four quadrants
ACMMG141

Investigate, with and without digital technologies, angles on a straight line, angles at a point and vertically opposite angles. Use results to find unknown angles
ACMSP144

Describe probabilities using fractions, decimals and percentages

AC9M5N04

Recognise that 100% represents the complete whole and use percentages to describe, represent and compare relative size; connect familiar percentages to their decimal and fraction equivalents
AC9M6N01

Recognise situations, including financial contexts, that use integers; locate and represent integers on a number line and as coordinates on the Cartesian plane
AC9M6N02

Identify and describe the properties of prime, composite and square numbers and use these properties to solve problems and simplify calculations
AC9M6N03

Apply knowledge of equivalence to compare, order and represent common fractions including halves, thirds and quarters on the same number line and justify their order
AC9M6N04

Apply knowledge of place value to add and subtract decimals, using digital tools where appropriate; use estimation and rounding to check the reasonableness of answers
AC9M6N05

Solve problems involving addition and subtraction of fractions using knowledge of equivalent fractions
AC9M6N06

Multiply and divide decimals by multiples of powers of 10 without a calculator, applying knowledge of place value and proficiency with multiplication facts; using estimation and rounding to check the reasonableness of answers
AC9M6N07

Solve problems that require finding a familiar fraction, decimal or percentage of a quantity, including percentage discounts, choosing efficient calculation strategies and using digital tools where appropriate
AC9M6N08

Approximate numerical solutions to problems involving rational numbers and percentages, including financial contexts, using appropriate estimation strategies
AC9M6N09

Use mathematical modelling to solve practical problems, involving rational numbers and percentages, including in financial contexts; formulate the problems, choosing operations and efficient calculation strategies, and using digital tools where appropriate; interpret and communicate solutions in te
AC9M6A01

Recognise and use rules that generate visually growing patterns and number patterns involving rational numbers
AC9M6A02

Find unknown values in numerical equations involving brackets and combinations of arithmetic operations, using the properties of numbers and operations
AC9M6M01

Convert between common metric units of length, mass and capacity; choose and use decimal representations of metric measurements relevant to the context of a problem
AC9M6M02

Establish the formula for the area of a rectangle and use it to solve practical problems
AC9M6M03

Interpret and use timetables and itineraries to plan activities and determine the duration of events and journeys
AC9M6M04

Identify the relationships between angles on a straight line, angles at a point and vertically opposite angles; use these to determine unknown angles, communicating reasoning
AC9M6SP02

Locate points in the 4 quadrants of a Cartesian plane
AC9M6SP03

Recognise and use combinations of transformations to create tessellations and other geometric patterns, using dynamic geometric software where appropriate
AC9M6P01

Recognise that probabilities lie on numerical scales of 0 – 1 or 0% – 100% and use estimation to assign probabilities that events occur in a given context, using common fractions, percentages and decimals

Teach Starter Publishing

We create premium quality, downloadable teaching resources for primary/elementary school teachers that make classrooms buzz!

1 Comment

Write a review to help other teachers and parents like yourself. If you'd like to request a change to this resource, or report an error, select the corresponding tab above.

No comments yet.