Add and subtract within 20, demonstrating fluency for addition and subtraction within 10. Use strategies such as counting on; making ten (e.g., 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); decomposing a number leading to a ten (e.g., 13 - 4 = 13 - 3 - 1 = 10 - ...
Add within 100, including adding a two-digit number and a one-digit number, and adding a two-digit number and a multiple of 10, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship b...
Understand that the three digits of a three-digit number represent amounts of hundreds, tens, and ones; e.g., 706 equals 7 hundreds, 0 tens, and 6 ones. Understand the following as special cases:
Interpret whole-number quotients of whole numbers, e.g., interpret 56 ÷ 8 as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 o...
Apply properties of operations as strategies to multiply and divide.2 Examples: If 6 × 4 = 24 is known, then 4 × 6 = 24 is also known. (Commutative property of multiplication.) 3 × 5 × 2 can be found by 3 × 5 = 15, then 15 × 2 = 30, or by 5 × ...
Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division (e.g., knowing that 8 × 5 = 40, one knows 40 ÷ 5 = 8) or properties of operations. By the end of Grade 3, know from memory all pr...
Multiply one-digit whole numbers by multiples of 10 in the range 10-90 (e.g., 9 × 80, 5 × 60) using strategies based on place value and properties of operations.
Understand a fraction 1/b as the quantity formed by 1 part when a whole is partitioned into b equal parts; understand a fraction a/b as the quantity formed by a parts of size 1/b.
Read and write multi-digit whole numbers using base-ten numerals, number names, and expanded form. Compare two multi-digit numbers based on meanings of the digits in each place, using >, =, and < symbols to record the results of comparisons.
Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangul...
Explain why a fraction a/b is equivalent to a fraction (n × a)/(n × b) by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. Use this principle to ...
Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model. Examples: 3/8 = 1/8 + 1/8 + 1/8 ; 3/8 = 1/8 + 2/...
Use decimal notation for fractions with denominators 10 or 100. For example, rewrite 0.62 as 62/100; describe a length as 0.62 meters; locate 0.62 on a number line diagram.
Use objects and pictorial models to solve
word problems involving joining, separating, and comparing sets within 20
and unknowns as any one of the terms in the problem such as 2 + 4 = [ ]; 3 + [ ] = 7; and 5 = [ ] - 3;
Use concrete and pictorial models to compose and
decompose numbers up to 1,200 in more than one way as a sum of so many thousands, hundreds, tens, and ones;
Add up to
four two-digit numbers and subtract two-digit numbers using mental strategies
and algorithms based on knowledge of place value and properties of operations;
Compose and decompose numbers up to 100,000
as a sum of so many ten thousands, so many thousands, so many hundreds, so many
tens, and so many ones using objects, pictorial models, and numbers, including
expanded notation as appropriate;
Represent
a number on a number line as being between two consecutive multiples of 10;
100; 1,000; or 10,000 and use words to describe relative size of numbers in
order to round whole numbers; and
Represent fractions greater than zero and
less than or equal to one with denominators of 2, 3, 4, 6, and 8 using concrete
objects and pictorial models, including strip diagrams and number lines;
Determine the corresponding fraction greater
than zero and less than or equal to one with denominators of 2, 3, 4, 6, and
8 given a specified point on a number line;
Explain that the unit fraction 1/b
represents the quantity formed by one part of a whole that has been partitioned
into b equal parts where b is a non-zero whole number;
Explain
that two fractions are equivalent if and only if they are both represented by
the same point on the number line or represent the same portion of a same size whole for
an area model; and
Represent multiplication facts by using
a variety of approaches such as repeated addition, equal-sized groups, arrays,
area models, equal jumps on a number line, and skip counting;
Use strategies and algorithms, including
the standard algorithm, to multiply a two-digit number by a one-digit number.
Strategies may include mental math, partial products, and the commutative, associative,
and distributive properties;
Decompose a fraction in more than one way
into a sum of fractions with the same denominator using concrete and pictorial
models and recording results with symbolic representations;
Use strategies and algorithms, including
the standard algorithm, to multiply up to a four-digit number by a one-digit
number and to multiply a two-digit number by a two-digit number. Strategies
may include mental math, partial products, a...
Practice working on specific math concepts with our set of 5 printable math graphic organizers.
Help Struggling Students with Math Graphic Organizers!
Graphic organizers are an essential tool in mathematics, specifically for young learners. Their visual framework greatly enhances comprehension and learning of otherwise abstract concepts. With these tools, students can categorize information, identify patterns, and establish relationships between mathematical ideas, developing logical reasoning and spatial awareness. This helps our youngest students grasp more complex math concepts quickly, laying a solid foundation for future success. In mathematics education, incorporating high-quality visual organization tools can be a total game-changer.
Pick a Printable Graphic Organizer for Math!
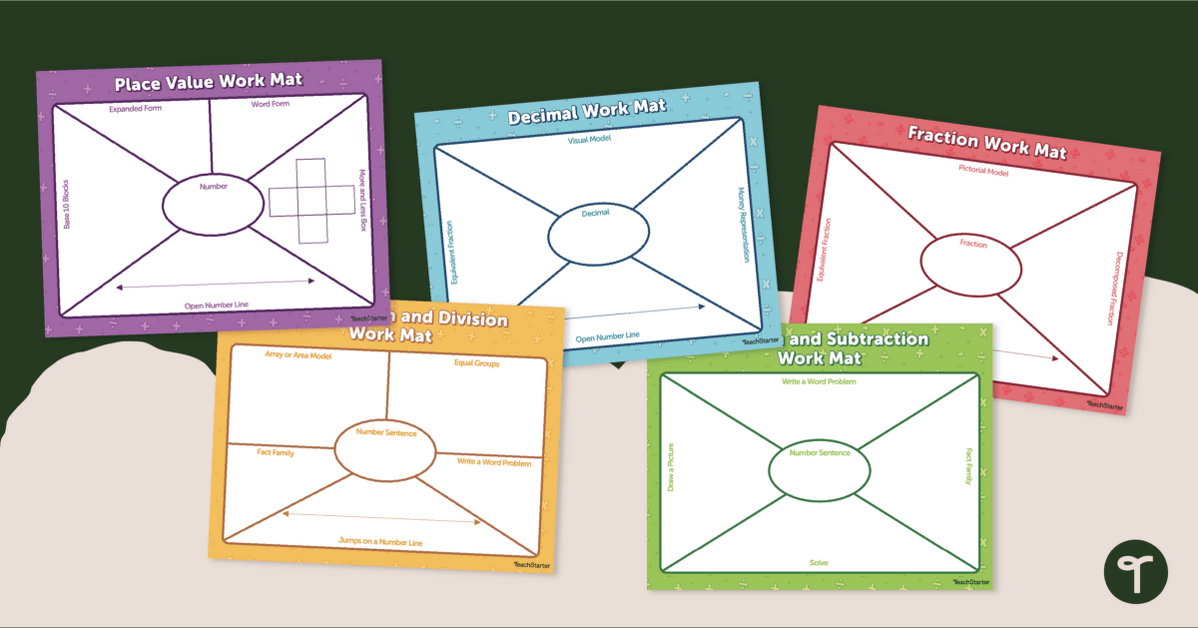
Use these work mats in your math class when working on the concepts of:
place value
addition and subtraction
multiplication and division
fractions
decimals.
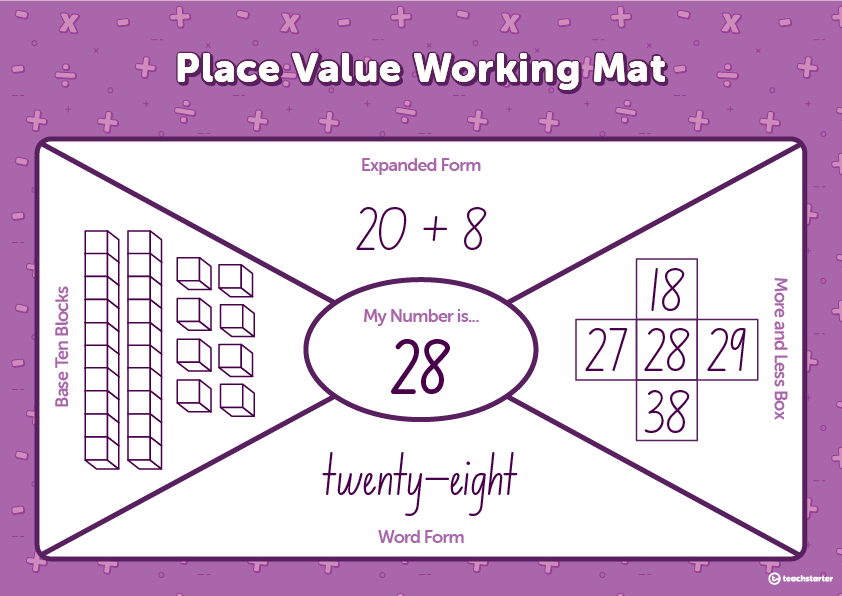
Each work mat has the students complete a series of tasks associated with that concept. These work mats are great to use with your guided math groups and when put in a math center. Simply slip a copy in a dry-erase sleeve so that your students can use a dry-erase marker and then wipe it clean.
Alternatively, project a copy on your dry-erase board to use as a whole class math warm-up.
Use the drop-down menu to choose between the color or black-and-white versions. This resource downloads as a PDF.
Add and subtract within 20, demonstrating fluency for addition and subtraction within 10. Use strategies such as counting on; making ten (e.g., 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); decomposing a number leading to a ten (e.g., 13 - 4 = 13 - 3 - 1 = 10 - ...
Add within 100, including adding a two-digit number and a one-digit number, and adding a two-digit number and a multiple of 10, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship b...
Understand that the three digits of a three-digit number represent amounts of hundreds, tens, and ones; e.g., 706 equals 7 hundreds, 0 tens, and 6 ones. Understand the following as special cases:
Interpret whole-number quotients of whole numbers, e.g., interpret 56 ÷ 8 as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 o...
Apply properties of operations as strategies to multiply and divide.2 Examples: If 6 × 4 = 24 is known, then 4 × 6 = 24 is also known. (Commutative property of multiplication.) 3 × 5 × 2 can be found by 3 × 5 = 15, then 15 × 2 = 30, or by 5 × ...
Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division (e.g., knowing that 8 × 5 = 40, one knows 40 ÷ 5 = 8) or properties of operations. By the end of Grade 3, know from memory all pr...
Multiply one-digit whole numbers by multiples of 10 in the range 10-90 (e.g., 9 × 80, 5 × 60) using strategies based on place value and properties of operations.
Understand a fraction 1/b as the quantity formed by 1 part when a whole is partitioned into b equal parts; understand a fraction a/b as the quantity formed by a parts of size 1/b.
Read and write multi-digit whole numbers using base-ten numerals, number names, and expanded form. Compare two multi-digit numbers based on meanings of the digits in each place, using >, =, and < symbols to record the results of comparisons.
Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangul...
Explain why a fraction a/b is equivalent to a fraction (n × a)/(n × b) by using visual fraction models, with attention to how the number and size of the parts differ even though the two fractions themselves are the same size. Use this principle to ...
Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model. Examples: 3/8 = 1/8 + 1/8 + 1/8 ; 3/8 = 1/8 + 2/...
Use decimal notation for fractions with denominators 10 or 100. For example, rewrite 0.62 as 62/100; describe a length as 0.62 meters; locate 0.62 on a number line diagram.
Use objects and pictorial models to solve
word problems involving joining, separating, and comparing sets within 20
and unknowns as any one of the terms in the problem such as 2 + 4 = [ ]; 3 + [ ] = 7; and 5 = [ ] - 3;
Use concrete and pictorial models to compose and
decompose numbers up to 1,200 in more than one way as a sum of so many thousands, hundreds, tens, and ones;
Add up to
four two-digit numbers and subtract two-digit numbers using mental strategies
and algorithms based on knowledge of place value and properties of operations;
Compose and decompose numbers up to 100,000
as a sum of so many ten thousands, so many thousands, so many hundreds, so many
tens, and so many ones using objects, pictorial models, and numbers, including
expanded notation as appropriate;
Represent
a number on a number line as being between two consecutive multiples of 10;
100; 1,000; or 10,000 and use words to describe relative size of numbers in
order to round whole numbers; and
Represent fractions greater than zero and
less than or equal to one with denominators of 2, 3, 4, 6, and 8 using concrete
objects and pictorial models, including strip diagrams and number lines;
Determine the corresponding fraction greater
than zero and less than or equal to one with denominators of 2, 3, 4, 6, and
8 given a specified point on a number line;
Explain that the unit fraction 1/b
represents the quantity formed by one part of a whole that has been partitioned
into b equal parts where b is a non-zero whole number;
Explain
that two fractions are equivalent if and only if they are both represented by
the same point on the number line or represent the same portion of a same size whole for
an area model; and
Represent multiplication facts by using
a variety of approaches such as repeated addition, equal-sized groups, arrays,
area models, equal jumps on a number line, and skip counting;
Use strategies and algorithms, including
the standard algorithm, to multiply a two-digit number by a one-digit number.
Strategies may include mental math, partial products, and the commutative, associative,
and distributive properties;
Decompose a fraction in more than one way
into a sum of fractions with the same denominator using concrete and pictorial
models and recording results with symbolic representations;
Use strategies and algorithms, including
the standard algorithm, to multiply up to a four-digit number by a one-digit
number and to multiply a two-digit number by a two-digit number. Strategies
may include mental math, partial products, a...
Represent the quotient of up to a four-digit
whole number divided by a one-digit whole number using arrays, area models,
or equations;
Teach Starter Publishing
We create premium quality, downloadable teaching resources for primary/elementary school teachers that make classrooms buzz!
0 Comments
Write a review to help other teachers and parents like yourself. If you'd like to
request a change to this resource, or report an error, select the corresponding tab
above.
Would you like something changed or customised on this resource? While our team
makes every effort to complete change suggestions, we can't guarantee that every
change will be completed.
0 Comments
Write a review to help other teachers and parents like yourself. If you'd like to request a change to this resource, or report an error, select the corresponding tab above.